UnitedMet harnesses RNA–metabolite covariation to impute metabolite ranges in medical samples

Knowledge preprocessing

This research complies with all related moral laws and was accepted by the institutional overview board at Memorial Sloan Kettering Most cancers Heart (MSKCC).

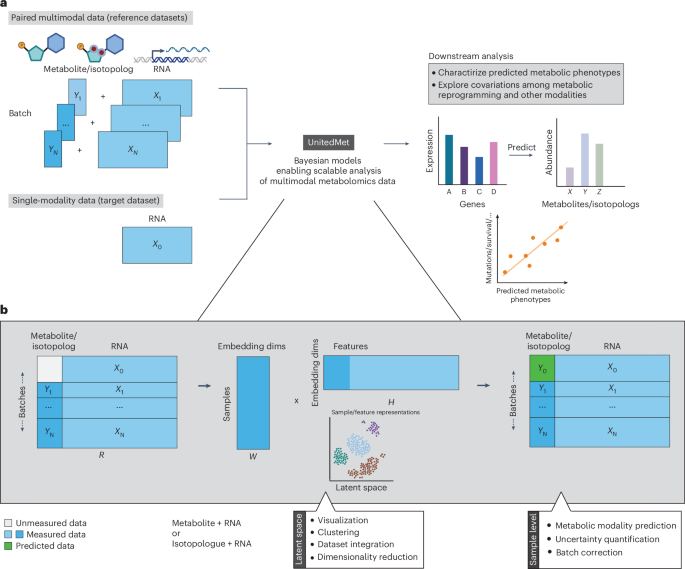
The enter to UnitedMet consists of reference datasets with paired measurements of RNA counts and complete ion counts of metabolites or isotopologs and a single-modality goal dataset with RNA-seq information solely (Fig. 1a). We assume that there are N completely different reference datasets, every with an RNA-seq pattern × gene matrix of uncooked counts ({X}_{n}in {{mathbb{R}}}^{{S}_{n}occasions {G}_{n}}(n=1,2,ldots ,N)) and a paired pattern × metabolite or pattern × isotopolog ion depend matrix ({Y}_{n}in {{mathbb{R}}}^{{S}_{n}occasions {M}_{n}}(n=1,2,ldots ,N)). Let ({X}_{0}in {{mathbb{R}}}^{{S}_{0}occasions {M}_{0}}) be the RNA-seq pattern × gene matrix in a single-modality goal dataset.

Normalization

We first normalized all enter information with distinct strategies. We applied complete ion depend normalization to uncooked ion depend matrices of metabolomics information (Y) and transcripts per million (TPM) normalization to uncooked depend matrices of RNA-seq information (X). In metabolomics experiments, ion counts beneath a threshold weren’t detected by the mass spectrometry. This ended up with lacking metabolite measurements in some samples. We handled these left-censored values as half of the minimal worth throughout all metabolite measurements when calculating the whole ion depend normalizer.

For pattern × isotopolog ion depend matrices (Y) of isotope labeling information, we first calculated the fractional labeling (specifically, the proportion of every isotopolog relative to the sum of all isotopologs in that metabolite). We then divided all fractions by the fraction of pyruvate M + 3 or glucose M + 6. Normalization by pyruvate M + 3 allowed us to determine the labeling ratio of every isotopolog to pyruvate M + 3, offering insights into the contribution of glucose-derived pyruvate to that particular isotopolog.The labeling ratio of citrate M + 2 to pyruvate M + 3, as an illustration, urged the contribution of glucose via the pyruvate dehydrogenase response. Normalization by glucose M + 6 as a substitute revealed the contribution of glucose carbon to different metabolites.

Rank transformation

As metabolomics and isotope tracing information generated utilizing mass spectrometry are reported as semiquantitative relative abundances, we’re solely capable of examine measurements of the identical metabolite or isotopolog from completely different samples in the identical dataset. To map metabolic relative abundances and gene expression ranges right into a shared measurement scale throughout all options and datasets, we rank the metabolite or isotopolog and gene expression ranges throughout all of the samples inside every dataset. Ranks allow the comparability of options throughout datasets and switch studying from RNA-seq modality to metabolic modality. Samples exhibiting the utmost stage for a particular function throughout the supplied dataset are assigned the very best rank. Conversely, samples displaying the minimal stage for a similar function are allotted the bottom rank. Left-censored samples are tied, sharing the final rank within the rating hierarchy. Whereas we use unnormalized rankings for modeling, we normalize ranks by their complete variety of samples S in downstream analyses, mapping them to a comparable scale of ranks [0, 1) in all datasets. Here, we use 𝑆 to refer to the number of samples within a dataset in a general sense, without referring to a specific dataset. For each feature j, the normalized rank of a measurement ({f}_{{ij}}(i=mathrm{1,2},ldots ,S;)) in that dataset is defined by ({rm{rank}}_{{ij}}=frac{{sum }_{k=1}^{S}P [;{f}_{{ij}} > {f}_{{kj}}]}{S}). Importantly, rank transformations are carried out individually for every metabolite, making certain that comparisons are made solely throughout the similar metabolite throughout samples. The ranked values are particular to every metabolite and will not be instantly comparable between completely different metabolites.

Knowledge aggregation

Rankings information of RNA-seq matrices X_n and metabolic matrices ({Y}_{n}(n=mathrm{1,2},ldots ,N)) in reference datasets are aggregated right into a single information matrix R together with the rankings information of metabolic matrix X₀ within the goal dataset. Whereas we take within the frequent genes shared throughout datasets to save lots of computation prices, we combination metabolic modalities by taking the union of related options (specifically, the aggregated matrix (Rin {{mathbb{R}}}^{{S}_{R}occasions {F}_{R}}), the place ({S}_{R}={S}_{0}+{sum }_{i=1}^{N}{S}_{n}) and ({F}_{R}=|{G}_{R}|+|{M}_{R}|,{G}_{R}={G}_{0}bigcap{cap }_{i=1}^{N}{G}_{i},{M}_{R}={cup}_{i=1}^{N}{M}_{i})). Within the benchmarking check on 4 ccRCC datasets, R contained measurements of 1,148 metabolites and 20,171 genes for 341 samples.

The UnitedMet mannequin

UnitedMet is a probabilistic generative technique that collectively fashions RNA-seq and metabolic information. UnitedMet assumes that the rankings in R are generated by a Plackett–Luce rating distribution of a latent variable matrix Z, the place (Z=WH) is the product of the latent pattern embedding matrix (Win {{mathbb{R}}}^{{S}_{R}occasions lambda }) and the latent function embedding matrix (Hin {{mathbb{R}}}^{lambda occasions {F}_{R}}). The hyperparameter λ is the variety of embedding dimensions. We suppose all latent variables in each latent embedding matrices are generated by regular prior distributions: ({W}_{{ik}}overset{textual content{iid}}sim {rm{Regular}}(mathrm{0,1}),{H}_{{kj}}overset{textual content{iid}}sim {rm{Regular}}(mathrm{0,1}),) the place W_ik is the entry within the ith pattern and the okth embedding column in embedding matrix W and H_kj is the entry within the okth embedding row and the jth function in embedding matrix H.

Plackett–Luce rating distribution

The Plackett–Luce distribution^46,47 fashions a rating of T objects as an ordered collection of decisions. It begins by selecting the top-ranked merchandise from your entire set of T choices, adopted by selecting the second-ranked merchandise from the remaining choices and so forth⁴⁸. Given a set of T choices ({{Q}_{1},ldots ,{Q}_{T}}), the likelihood of choosing the ith merchandise Q_i is outlined as (P(i|{1,ldots ,T})=frac{{u}_{i}}{{sum }_{t=1}^{T}{u}_{t}}) by the Luce alternative axiom, the place u_i represents the utility rating of Q_i. The likelihood of a full ordering ({{sigma }_{1},ldots ,{sigma }_{T}}), the place we assume ({Q}_{{sigma }_{1}} > ldots > {Q}_{{sigma }_{T}}), is then given by recursively making use of the Plackett–Luce distribution, selecting σ₁ from ({1,ldots ,T}), σ₂ from ({1,ldots ,T}backslash {{sigma }_{1}}) and σ₃ from ({1,ldots ,T}backslash {{sigma }_{1},{sigma }_{2}}), yielding (P({{sigma }_{1},ldots ,{sigma }_{T}}|{1,ldots ,T})={prod }_{i=1}^{T}frac{{u}_{{sigma }_{i}}}{{sum }_{r=i}^{T}{u}_{{sigma }_{r}}}). Given the latent variable matrix (Z=WH) in UnitedMet, we suppose the utility rating of the merchandise within the ith pattern and the jth function is outlined as ({rm{exp}}({Z}_{ij})={rm{exp}}({{W}_{i}}{H}_{j})). Extending this to censored rankings in UnitedMet, the chance of observing a censored ordering ({{sigma }_{1},{sigma }_{2},ldots ,{sigma }_{Ok},{{sigma }_{Ok+1},ldots ,{sigma }_{S}}}) within the jth function of a batch is then outlined by (Pleft({R}_{!j}=left{{Z}_{{sigma }_{1},,j} > {Z}_{{sigma }_{2},,j} > ldots > {Z}_{{sigma }_{Ok},,j} >proper.proper.) (left.left.{{Z}_{{sigma }_{Ok+1},,{j}},ldots ,{Z}_{{sigma }_{S},,{j}}}proper}|{{Z}_{1,,{j}},ldots ,{Z}_{S,,{j}}}proper))(={prod }_{i=1}^{Ok}frac{{rm{exp}}({Z}_{{sigma }_{i},,{j}})}{{sum }_{r=i}^{S}{rm{exp}}({Z}_{{sigma }_{r},,{j}})}). Detailed definitions of UnitedMet are described beneath.

Cross-validation

To find out the optimum variety of embedding dimensions ((lambda)) of latent matrices (W) and (H), we use tenfold cross-validation. The vary of (lambda) to be examined is contingent on the whole variety of samples ({S}_{R}). As an illustration, efficiency analysis spans a (lambda) vary of [1, 351] with a step of 10 within the benchmarking check on ccRCC datasets. For every batch, cross-validation options which can be used to check mannequin efficiency are chosen individually. Solely metabolic options (metabolites or isotopologs) which can be measured in at the least one different batch are included. These options are then randomly distributed into ten folds. We deal with one fold at a time as unmeasured and maintain out the fold’s options within the corresponding batch. Masked options are then predicted by UnitedMet. In the long run, we calculate the imply absolute error (MAE) between the true ranks of held-out options within the fold and their predicted ranks. The MAE scores throughout all folds are averaged to acquire a closing efficiency rating. We consider the MAE scores for all (lambda) values and the one ensuing within the elbow of the MAE rating curve is chosen because the optimum variety of embedding dimensions for the factorization.

Inference

The chances are computed from noticed rankings in each paired modalities of reference datasets and solely within the respective RNA-seq modality of the goal dataset. We use SVI throughout the Pyro⁴⁹ bundle for inference. Variational distributions are generated utilizing the AutoNormal perform. Optimization is executed via the Adam optimizer, with a default studying charge set to 0.001. Convergence is ascertained when the relative change in proof decrease certain (ELBO) falls beneath 0.01. To handle the inherent imbalance between the RNA-seq and metabolomics modalities in eventualities the place we need to impute a big panel of metabolites from a subset of measured metabolites and RNA-seq information, we launched a weighted loss perform in UnitedMet. Usually, RNA-seq information comprises measurements for about 20,000 genes, whereas metabolomics information includes round 1,000 measured metabolites. This huge distinction within the variety of options between the 2 modalities can disproportionately have an effect on the chance computation, resulting in biases within the inferred rankings. To mitigate this situation, we utilized modality-specific weighting when computing the log-likelihood utilizing the Plackett–Luce distribution. Particularly, we assigned equal weight to the metabolomics options, whereas down-weighting the gene options proportionally by the ratio of the variety of metabolites to genes. Given a log-likelihood matrix L of form (n_genes + n_metabolites) × S, the place S is the variety of samples. We outlined a weight matrix C of the identical form such that: C_:,j = 1, if j corresponds to a metabolite; C_:,j = n_metabolites/n_genes, if j corresponds to a gene. The weighted log-likelihood matrix was computed as: L_weighted = C ⊙ L. The ultimate complete log-likelihood was obtained by summing over all noticed values in L_weighted.

Posterior prediction

UnitedMet estimates the joint posterior distribution of the latent embedding matrix (W) and (H). For each latent variable in (W) and (H), we draw 1,000 samples from their estimated posterior distribution. Given posterior samples of the latent matrix (Z(=WH)), posterior rankings are then generated by the Plackett–Luce rating distribution. To pattern in a computation-efficient manner, we applied the Gumbel–Max trick⁵⁰, which generates ordered samples from the Plackett–Luce rating distribution by sorting the perturbed log likelihood via the addition of impartial variables from the Gumbel distribution⁵¹ (({G}_{1,,j},ldots ,{G}_{S,,j}sim {rm{Gumbel}}(0),{rm{iid}})). Let ({Z}_{,;j}) be the ({j}{rm{th}}) column of the latent matrix (Z). Set perturbed log likelihood ({U}_{i,j}) = ({Z}_{i,j}+{G}_{i,j}). The ordered indices of the ({j}{rm{th}}) column returned by sorting the perturbed log possibilities ({{U}_{1,,j},ldots ,{U}_{S,,j}}) are equal to the orderings generated by the Plackett–Luce mannequin given possibilities (utility scores) ({{Z}_{1,;j},ldots ,{Z}_{S,;j}}). Particularly, if ({{U}_{{sigma }_{1},,j} > {U}_{{sigma }_{2},,j} > ldots > {U}_{{sigma }_{Ok},,j} > {{U}_{{sigma }_{Ok+1},,j},ldots ,{U}_{{sigma }_{S},,j}}}), then we observe ({{Z}_{{sigma }_{1},;j} > {Z}_{{sigma }_{2},;j} > ldots > {Z}_{{sigma }_{Ok},;j} > {{Z}_{{sigma }_{Ok+1},;j},ldots ,{Z}_{{sigma }_{S},;j}}}).

Estimates of the rankings could be discovered because the imply of the 1,000 posterior attracts, whereas the s.d. of posterior samples represents a quantification of the prediction uncertainty.

Benchmarking

Multivariate Lasso regression

We applied multivariate Lasso regression on 4 ccRCC datasets in keeping with Li et al.²¹. In every dataset, metabolomics information had been preprocessed by complete ion depend normalization, whereas transcript ranges had been transformed into TPM items. At every time within the benchmarking experiments, one ccRCC dataset was handled because the testing set whereas the opposite three had been coaching units. All RNA-seq information had been scaled earlier than coaching or testing. For each metabolite (y), we used gene expressions (x) to foretell it within the coaching set. LassoCV in Python bundle scikit-learn was used to pick out one of the best penalizer α by fivefold cross-validation. The utmost variety of iterations becoming alongside the regularization path was set to default 1,000. After selecting the right mannequin for every metabolite, we assessed mannequin accuracy by calculating Spearman correlation coefficients between predicted metabolite ranges and their floor truths.

MIRTH

MIRTH is a matrix factorization method geared toward predicting the degrees of unmeasured metabolites by collectively analyzing the covariation of metabolites throughout a number of datasets²³. We prolonged MIRTH to the cross-modality prediction drawback as beforehand described²². Metabolomics and RNA-seq information had been preprocessed in the identical manner talked about above.

MSKCC ccRCC datasets

We obtained two datasets, RC18 (n = 144) and RC20 (n = 76), every with matched RNA-seq and mass spectrometry metabolomics measurements from recent frozen high-quality tumor or adjoining regular specimens of individuals with ccRCC that underwent partial or radical nephrectomies at MSKCC²². Samples had been collected below the approval of MSKCC’s institutional overview board. The alignment of RNA-seq reads was carried out utilizing STAR two-pass alignment in opposition to human genome meeting hg19. Metabolites had been recognized on the idea of the factors in keeping with Benedetti et al.¹⁴. RC18 had measurements for 783 metabolites and 22,937 genes. RC12 had measurements for 1,012 metabolites and 22,987 genes.

CPTAC ccRCC datasets

Metabolite uncooked depend matrices of CPTAC (n = 50) and CPTAC_val (n = 71) had been downloaded from Li et al.¹. Transcriptomic and WES information had been downloaded from Genomic Knowledge Commons (https://portal.gdc.most cancers.gov/tasks/CPTAC-3; venture: CPTAC-3, major website: kidney). CPTAC contained solely ccRCC tumor samples, whereas CPTAC_val contained tumor and adjoining regular samples of individuals with ccRCC. Mass spectrometry peaks had been quantified utilizing Thermo Scientific Compound Discoverer software program to generate uncooked counts. HTSeq model 0.11.2 was applied to calculate the gene-level stranded learn depend. We then carried out complete ion depend normalization and TPM normalization on metabolite and gene expression depend matrices, respectively. CPTAC had measurements for 183 metabolites and 60,483 genes. CPTAC_val had measurements for 130 metabolites and 60,483 genes.

Breast most cancers datasets

Matched TPM-normalized RNA-seq and bulk metabolomic information (uncooked depend matrices) of two breast most cancers datasets BrCa1 (ref. ²⁴) (n = 108, no. of metabolites = 533, no. of genes = 20,032), BrCa2²⁵ (n = 18, no. of metabolites = 397, no. of genes = 21,773) had been downloaded from Benedetti et al.¹⁴. RNA-seq information of major tumor tissues from the TNBC cohort (n = 360, no. of genes = 23,211) had been downloaded from the Nationwide Omics Knowledge Encyclopedia (https://www.biosino.org/node/evaluation/element/OEZ00000398) in keeping with Jiang et al.²⁷. Bulk metabolomics information of the TNBC cohort (n = 479, no. of metabolites = 594) had been downloaded from Xiao et al.²⁶. There have been 258 tumor samples with paired RNA-seq and metabolomics information after matching.

Human RCC RNA-seq and isotopic labeling information infused with [U-¹³C]glucose in vivo

Paired RNA-seq and isotopic labeling information from 76 major tumor or adjoining regular kidney samples of individuals with RCC had been downloaded from Bezwada et al.²⁸. The RCC dataset had measurements for 64 isotopologs and 12,300 genes. As a result of small fluctuations of isotopolog ranges that aren’t biologically interpretable could be quantified as indicators in mass spectrometry, we set a criterion to filter out isotopologs whose common fraction over all samples was lower than 10%. This ended with a complete of 23 isotopologs together with biologically significant isotopologs comparable to citrate M + 2 and malate M + 2.

Human NSCLC cell line RNA-seq and isotopic labeling information

We downloaded two human NSCLC cell line datasets with paired RNA-seq and isotopic labeling information from Chen et al.³: NSCLC-G (n = 85, no. of isotopologs = 28, no. of genes = 16,383) and NSCLC-Q (n = 85, no. of isotopologs = 21, no. of genes = 16,383). A complete of 85 NSCLC cell strains had been cultured with medium containing the isotopically enriched nutrient below equivalent situations. The isotopic information in NSCLC-G had been labeled with [U-¹³C]glucose, whereas the isotopic information in NSCLC-Q had been labeled with [U-¹³C]glutamine. After filtering out isotopologs whose common fraction over all samples was lower than 10%, there have been 9 and eight isotopologs within the NSCLC-G and NSCLC-Q datasets, respectively.

TCGA datasets

We downloaded paired RNA-seq, WES and medical information of 1,020 RCC tumor and adjoining regular samples in TCGA KIPAN from the Genome Knowledge Evaluation Heart (GDAC) at Broad Institute. A complete of 606 TCGA KIRC samples had been included in TCGA KIPAN. mtDNA mutation calls utilizing a PCR-based amplification method for 61 ChRCC circumstances in TCGA KICH had been downloaded from Davis et al.²⁹. Paired RNA-seq, WES and medical information of TCGA LUAD (n = 576) had been additionally downloaded from GDAC.

Annotation of MAF information from WES information

We downloaded MAF information of WES information for CPTAC, CPTAC_val, TCGA KIPAN and TCGA KIRC from the corresponding web sites talked about above. We annotated all molecular variations to 0 or 1 in a gene-wise manner, the place 0 represented wild-type or silent variations and 1 represented nonsilent variations. Missense mutation, nonsense mutation, frame-shift deletion, splice website mutation, frame-shift insertion, in-frame deletion, splice-region variant, translation begin website mutation, in-frame insertion and nonstop mutation had been thought-about as nonsilent molecular variations. Silent mutations, intron mutation, 3′ UTR mutation and 5′ UTR mutation had been thought-about as silent variations, as a result of they weren’t capable of change gene features.

DA rating

The DA rating assesses the distinct regulation of a metabolic pathway between two teams. Calculated via a Wilcoxon rank-sum check utilized to all pathway metabolites, the rating undergoes P-worth correction utilizing the Benjamini–Hochberg technique (FDR-corrected P worth 

Survival evaluation

We collected RNA-seq information and participant-level medical info from IMmotion151 (refs. ^35,52) (n = 823), a printed trial exploring immunotherapeutic versus systemic brokers in superior ccRCC. To account for various drug results in medical trials, we carried out separate statistical analyses for the immunotherapy arm (atezolizumab + bevacizumab) and the sunitinib arm. The survival regression evaluation was carried out utilizing the Python bundle lifelines.

Statistical and reproducibility

Statistical analyses had been carried out utilizing both R or Python. Differential distribution comparisons had been applied with the Wilcoxon rank-sum check or t-test. All statistical checks had been two-sided by default, until specified in any other case, with P values corrected utilizing the Benjamini–Hochberg technique⁵³. No statistical technique was used to predetermine pattern measurement and no information had been excluded from the analyses. Blinding and randomization weren’t related as a result of this was an observational research.

Reporting abstract

Additional info on analysis design is offered within the Nature Portfolio Reporting Abstract linked to this text.